¶ Definition der Menge
Unter einer Menge verstehen wir jede Zusammenfassung M von bestimmten wohlunterschiedenen Objekten m unserer Anschauung oder unseres Denkens (welche "Elemente" von M genannt werden) zu einem Ganzen. [1, S. 1, 1.1.1]
Eine Menge ist also grob eine Auflistung bzw. Zusammenfassung von Dingen bzw. Objekten, Objekt kann dabei alles sein: Gegenstände, Emotionen, Abstraktes wie Zahlen, Symbole [1, S.2, Abschnitt 1.1.3] , oder Buchstaben, Gedanken, etc. (für die Herkunft des Begriffs ist die Subjekt-Objekt-Spaltung von Karl Jaspers zu empfehlen: https://de.wikipedia.org/wiki/Subjekt-Objekt-Spaltung). In der Mathematik werden hier meist abstrakte, mathematische Objekte in Mengen gedacht. So können Zahlen oder Variablen in Mengen enthalten sein, jedoch auch die Menge selbst, wodurch eine Art Verschachtelung entstehen kann. Wichtig ist, dass die Objekte oder Elemente in einer und der selben Menge wohlunterschieden, also nicht gleich sein müssen[1, S.1, 1.1.1.(3)]. Dabei sei zu beachten, dass man Mengen mit Zahlen und Mengen richtig zu unterscheiden weiß. Beispiel:
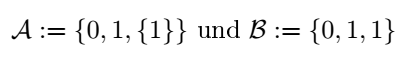
Menge A ist in diesem Fall korrekt, da 1 und die Menge mit der Zahl 1, zwei wohlunterschiedene Objekte sind. Menge B ist nicht korrekt, weil 1 und 1 identisch also nicht wohlunterschieden sind. Ab wann Objekte in Mengen genau wohlunterschieden sind folgt im Artikel weiter unten [commung soon].
¶ Explizite und deskriptive Mengenbeschreibung
¶ Explizite Darstellung
Die explizite Darstellung einer Menge besteht darin, dass man die einzelnen Elemente mit Komma getrennt auflistet und dann mit geschweiften Klammern eingeklammert [1, S1., 1.1.2]. Die Menge A und B definieren sich (Definitionen nutze " := " und keine einfaches " = "!) als Beispiel wie folgt:
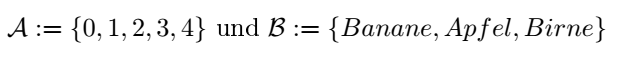
Es gibt auch die "..."-Schreibweise, sie wird verwendet, wenn man eine endliche mengen abkürzen möchte oder um unendliche Mengen explizit darstellen zu können. Diese Schreibweise ist jedoch nur da zulässig, wo man auch eine deskriptive Schreibweise verwenden könnte [1, S.2, 1.1.2]. In Mathe A wird diese Verkürzung jedoch nicht gerne gesehen, da man das Darstellen von "deskriptiven Mengen" lernen / üben soll.
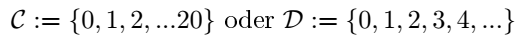
¶ Deskriptive Darstellung
Wir haben ein Menge B welche wir nicht explizit, also durch Aufzählung definieren wollen, sondern mit Hilfe einer Aussage A (eine Aussage ist nach Aristoteles "ein sprachliches Gebilde, von dem es sinnvoll ist, zu sagen, es sei wahr oder falsch [...]" [1, S.2, 1.1.4]). Wenn die Aussage A wahr ist, dann wissen wir, dass wir unser zu prüfendes Objekt x in der Menge vorkommt, andersherum also, wenn A falsch ist, dann wissen wir, dass das Objekt also x nicht in der Menge vorkommt. Damit klar ist welches Objekt wir in der Aussage denn überhaupt prüfen wollen schreiben wir es in Klammern hinter das A also: A(x). Die deskriptive Darstellung sind im ganzen wie folgt aus:
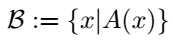
Zur Erläuterung - was sich wie erwähnt, zur expliziten Darstellung ändert ist der Inhalt in den Klammer. x ist ein Platzhalter oder Variable für ein beliebiges Objekt, welches man prüfen möchte, dieses wird dann von der Aussage A(x) mit einem " | " getrennt. [1, S.3 , 1.1.5]
¶ Zahlenmengen

Fehler in der Definition rationaler Zahlen: es muss heißen: Es gibt y, z mit y aus Z und z aus Z und z ≠ 0 und x = y / z [1, S. 4, 1.1.8]
¶ binäre Vereinigung, binärer Durchschnitt, Differenz
Seien A und B Mengen:
(1.) binäre Vereinigung: "A vereinigt mit B": Alle Elemente die in A und oder in B sind. (Abb. 6, oben links)
(2.) binärer Durchschnitt: "A geschnitten mit B": Alle Elemente die in A und in B sind. (Abb. 6, oben rechts)
(3.) Differenz:
- "A ohne B": Alle Elemente die in A sind und nicht in B sind. (Abb. 6, unten links)
- "B ohne A": Alle Elemente die in B sind und nicht in A sind. (Abb. 6, unten rechts)
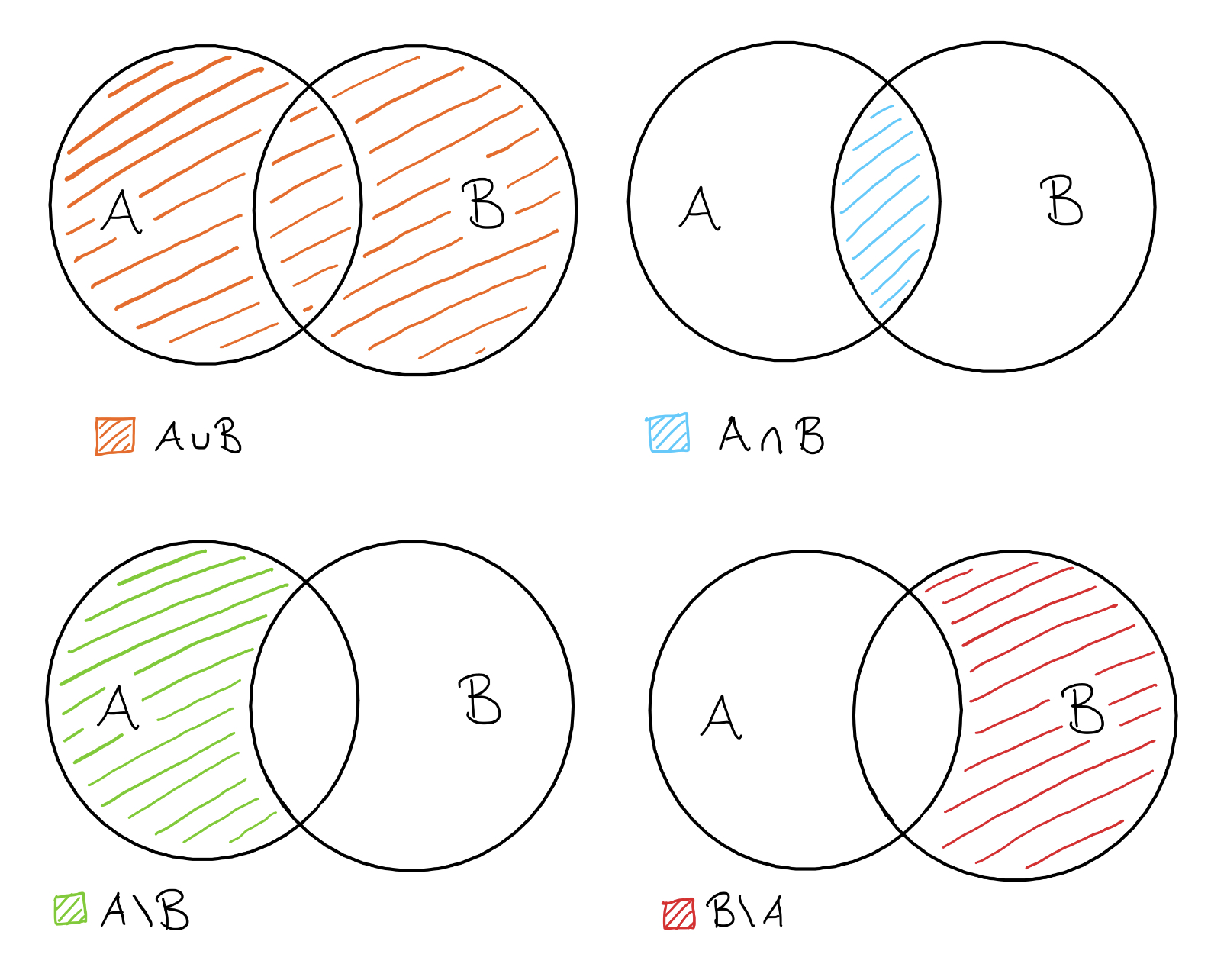
[1, S.7-8, 1.2.1]
¶ Referenzen
[1] Rudolf Berghammer, "Mathematik für die Informatik, Grundlegende Begriffe, Strukturen und ihre Anwendung", Springer Vieweg, 2. Auflage.
[2] Albrecht Beutelspacher, " 'Das ist o. B. d. A. trivial!', Tipps und Tricks zur Formulierung mathematischer Gedanken", Vieweg+ Teubner, 9. Auflage.